遠山競輪研究所

直近4ヶ月得点・最近の調子と今場所成績の関係( 2023/04/07 )
競輪の車券予想において、選手の直近4ヶ月得点(直近4ヶ月の平均競走得点)や最近の調子(競走得点の上昇・下降)が重要視されることも多いのですが、実際には選手の得点や調子はどの程度レース結果に反映されるのでしょうか。
今回は、選手の直近4ヶ月得点・最近の調子と今場所成績の関係を調査し、的確に選手の実力を判定する方法を検討しました。
なお検討過程は統計的手法を使った分析が続くのですが、興味の無い方には読みづらいかもしれません。とりあえず結果だけ知りたいという方は、最初と最後の項目である1.直近4ヶ月得点・最近の調子と今場所成績 と、6.まとめ をお読みください。
以下目次項目
1. 直近4ヶ月得点・最近の調子と今場所成績
「直近4ヶ月得点」とは、出走表の「競走得点」の項目に記載されている数値で、直近4ヶ月間に出走したレースで得た競走得点の平均値です。正式には「直近4ヶ月の平均競走得点」ですが、ここでは短縮形で「直近4ヶ月得点」と呼びます。
「最近の調子」については公式に定められた定義はないのですが、ここでは「直近3場所得点(直近3場所の平均競走得点)」と「直近4ヶ月得点」の差とします(図1 の赤矢印)。最近の調子が良ければ(直近3場所得点が直近4ヶ月得点を上回っていれば)プラス値となるし、最近の調子が悪ければマイナス値となります。
※ 最近の調子=直近3場所得点 − 直近4ヶ月得点
「今場所成績」として、今回は「今場所得点」(今場所の平均競走得点)を用います。
それぞれの関係を図的に表現したのが図1です。
図において青丸は1開催に該当し、青丸のY座標(高さ)はその開催で得られた平均競走得点を意味します。
図1. 直近4ヶ月得点、直近3場所得点および今場所得点
直近3場所得点
直近4ヶ月得点
最近の調子
得点
95.0
94.0
93.0
92.0
91.0
90.0
1前回
2前回
3前回
直近4ヶ月
今場所成績
B
A
C
上振れ
下振れ
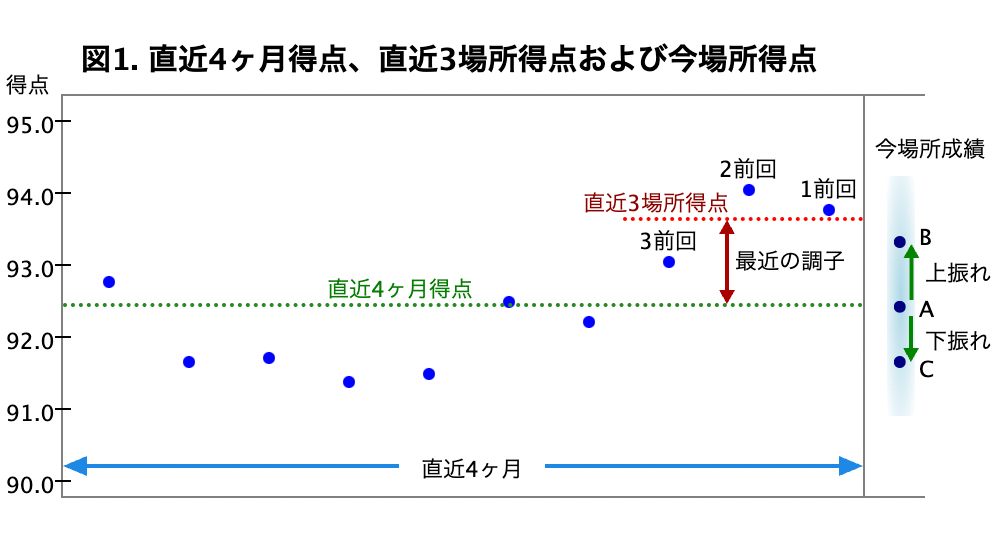
一般的に選手実力の判定に直近4ヶ月得点(図1における緑破線)が使われます。
今場所も実力どおりの成績であれば、今場所成績は理論上では直近4ヶ月得点と同じになります(図1のA点)。
さて、最近の調子が良ければ今場所成績は上振れして直近4ヶ月得点より上側(例えば図1のB点)、最近の調子が悪ければ今場所成績は下振れして直近4ヶ月得点より下側(例えば図1のC点)となるのでしょうか?
以下で、これらのことについて検証していきます。
2. 相関係数について
今回は今場所成績と過去成績(直近4ヶ月得点 および 最近の調子)の関係を調べるのに「相関係数」を使って判断しています。
よって、ここで相関係数について簡単に説明しておきます。
相関係数とは、二つのデータの比例関係を表す係数で、1 から −1 の間の数で表します。
相関係数の絶対値が 1 に近いほど、相関関係が強くなります。
一般的に、相関係数の大きさで相関関係は次のように解釈されます。
| 相関係数の絶対値 | 解釈 |
|---|---|
| 0.0 ~ 0.2 | ほとんど相関関係がない |
| 0.2 ~ 0.4 | やや相関関係がある |
| 0.4 ~ 0.7 | かなり相関関係がある |
| 0.7 ~ 1.0 | 強い相関関係がある |
以下の調査においては、計算で得られた相関係数について、t 検定で得られた p値が 0.1を超えた場合(危険率が10%を超えた場合)は、「サンプル数が十分ではなく、計算した相関係数は無効」と判断して、相関係数を ‘----’ に置き換えて表記しています。
(p値が 0.05~0.10の場合は、相関係数値の右上に✶印を付加するが、今回は該当が無かった)
3. 直近4ヶ月得点と今場所得点の関係
昨年(2022年)の1年間のA12班戦レースで、出走選手の直近4ヶ月得点と今場所得点の関係をプロットした散布図です。
対象は以下の条件を満たす選手で、該当選手は延べ人数で 8,194人です。
- ・直近4ヶ月と今場所がA12班
- ・直近3場所間に60日以上の長欠がない
- ・直近4ヶ月間で6場所以上の出走がある
- ・今場所、最終日まで出走した
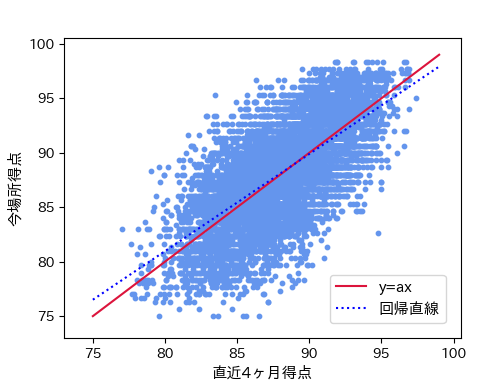
当然、今場所得点は直近4ヶ月得点どおりとはならず、レース展開等によってバラツキが生じるのですが、ある程度の関係性が見られます。
相関係数を計算すると r=0.673 となり、「かなり相関関係がある」レベルとなります。
回帰分析で求めた回帰直線(青点線)は、
y=0.892x + 9.60 (決定係数 r2=0.453)
であり、今場所得点=直近4ヶ月得点 である赤線(y=ax)とほぼ一致します。
実際のレース予想において選手実力として直近4ヶ月得点を用いることは妥当だと思われます。
ちなみに、回帰分析で得た 決定係数 r2=0.453 が意味するところは、「今場所成績の 45.3%は直近4ヶ月得点で説明できるが、残り54.7%はレース展開等の他の要素が影響する」ということです。
(選手実力として直近4ヶ月得点を用いた場合、A12班戦レースは 実力が 45%、展開等の他の要素が 55%)
他のクラスについても、同様に昨年(2022年)の1年間のレースデータで得られた分析結果を下表にまとめておきます。
他クラスの回帰直線も傾きが0.9前後で y=ax と近似しており、選手実力として直近4ヶ月得点を用いることに問題はありません。
ただ注目すべきはガールズ戦の決定係数は r2=0.690 と高いことです。つまりガールズ戦では、「今場所成績の 69%は直近4ヶ月得点で説明でき、レース展開等の影響は 31%に留まる」ということです。
(選手実力として直近4ヶ月得点を用いた場合、ガールズ戦は 実力が 69%、展開等の他の要素が 31%)
表3. 直近4ヶ月得点 と 今場所得点 の相関関係
| S級戦 ※ | A12班戦 | チャレンジ戦 | ガールズ戦 | ||
|---|---|---|---|---|---|
| 該当選手数(延べ人数) | 7,844 | 8,194 | 7,612 | 3,008 | |
| 直近4ヶ月得点 の分布データ | 平均値 | 101.26 | 88.22 | 70.31 | 50.70 |
| 標準偏差 σ | 4.69 | 3.29 | 3.40 | 3.29 | |
| 今場所得点 の分布データ | 平均値 | 101.19 | 88.30 | 70.41 | 50.78 |
| 標準偏差 σ | 5.31 | 4.36 | 4.36 | 3.75 | |
| 相関係数 r | 0.757 | 0.673 | 0.722 | 0.831 | |
| 回帰直線 (y=ax+b) | 傾き(a) | 0.858 | 0.892 | 0.926 | 0.946 |
| 切片(b) | 14.31 | 9.60 | 5.31 | 2.81 | |
| 決定係数 r2 | 0.573 | 0.453 | 0.522 | 0.690 | |
※S級戦については、番組構成による得点の差が出ないよう、今場所はF1戦のみを対象としています。
ただし、直近4ヶ月得点および直近3場所得点にはグレードレースも含まれます。

4. 最近の調子と今場所成績の上振れ/下振れ
次に最近の調子(図1の赤矢印)と、今場所成績の上振れ/下振れ(図1の緑矢印)の関係を調べます。
最近の調子が今場所も続くようであれば、両者の間には相関関係が見られるはずです。
昨年(2022年)の1年間のA12班戦レースで、出走選手の「最近の調子」と「今場所成績の上振れ/下振れ」の関係をプロットした散布図です。
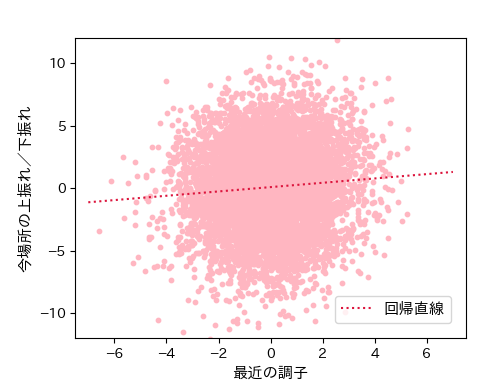
上で調査した「直近4ヶ月得点と今場所得点の関係」と違って、最近の調子と今場所成績の上振れ/下振れの間には関係性が見られません。
相関係数も r=0.080 であり、正の値なので「好調(不調)であれば今場所成績は上がる(下がる)」という多少の傾向はありますが、「ほとんど相関関係がない」というレベルです。
つまり、全体としては「最近の調子が今場所成績に与える影響はほとんどない」ということを示しており、意外な結果でした。
「最近の調子が上がる(下がる)と 直近4ヶ月得点にも反映されるので、それ以上のプラス(マイナス)はあまり考えなくても良い」とか、
「選手の3場所程度の好調・不調は偶発的なもので長続きしない」と解釈すべきでしょうか。
(選手実力の判定には積分的要素である直近4ヶ月得点が重要であり、微分的要素である最近の調子を過度に考慮するのは危険!)
他クラス分を含めて、調査結果を表4 にまとめておきます。
どのクラスでも同様の結果(相関係数は 0.08前後、回帰直線の係数は 0.15~0.18程度)でした。
表4. 最近の調子 と 今場所成績の上振れ/下振れ の相関関係
| クラス | S級戦 | A12班戦 | チャレンジ戦 | ガールズ戦 | |
|---|---|---|---|---|---|
| 対象選手数(延べ人数) | 7,844 | 8,194 | 7,612 | 3,008 | |
| 相関係数 | 0.074 | 0.080 | 0.083 | 0.075 | |
| 回帰直線 (y=ax+b) | 傾き(a) | 0.154 | 0.174 | 0.183 | 0.164 |
| 切片(b) | -0.083 | 0.085 | 0.104 | 0.085 | |

5. 「最近の調子」の反映について、もう少し調べてみる
上の分析結果では、「最近の調子が今場所成績に与える影響はほとんどない」ということでしたが、実際には「好調な若手選手が右肩上がりでどんどん成績を上げていく」という状況は良く目にしますし、車券検討では「そういった選手の実力は出走表の直近4ヶ月得点より上にあると見たほうが正解」となることが多いようです。
条件によっては「最近の調子」を「今場所成績の予測」に反映させるべきなのではないでしょうか?
ということで、
- 1. 選手の年齢
- 2. 直近3場所の勝率
の分類条件を加えて、「最近の調子」と「今場所成績の上振れ/下振れ」の関係を再調査してみました。
5-1.選手の年齢別の調査
クラス毎に選手年齢別の「最近の調子」と「今場所成績の上振れ/下振れ」の相関係数を調べた結果の表です。
今まで同様に2022年の1年分のレースが調査対象であり、表の( )内の数値は該当選手数(延べ人数)です。
相関係数が 0.1を超える部分に黄色のマーカーを引いています。
表5-1. 選手年齢別の相関係数
| 選手年齢 | S級戦 | A12班戦 | チャレンジ戦 | ガールズ戦 |
|---|---|---|---|---|
| 25歳以下 | 0.070 (693) | 0.164 (392) | 0.131 (687) | 0.018 (1,341) |
| 26歳~30歳 | 0.059 (1,072) | 0.128 (870) | 0.162 (377) | 0.070 (800) |
| 31歳~40歳 | 0.069 (3,613) | 0.070 (3,342) | 0.061 (2,011) | 0.156 (635) |
| 41歳以上 | 0.090 (2,466) | 0.066 (3,590) | 0.080 (4,537) | 0.165 (232) |
A12班戦・チャレンジ戦にはおいては 30歳以下の選手では相関係数が 0.1を超えてきます。
S級戦では年齢帯によって相関係数が大きくなるという傾向は見られませんでした。
「チャレンジ戦でデビューする男子選手は、本来の自分の実力の位置までは右肩上がりで成績が上がっていく」ということが現れているのでしょうか。
ガールズ戦では逆に30歳以下で相関係数が低く、31歳以上で相関係数が高くなっています。
ガールズ選手はデビュー直後からトップ選手と対戦することになるのが影響しているのでしょう。
いずれにしても、年齢別では一つの目安となる「相関係数 0.2 以上」の領域はありませんでした。
5-2.直近3場所の勝率別の調査
クラス毎に直近3場所の勝率別の「最近の調子」と「今場所成績の上振れ」の相関係数を調べた結果の表です。
2022年の1年分のレースが調査対象であり、表の( )内の数値は該当選手数(延べ人数)です。
相関係数が 0.1を超える部分に黄色のマーカーを、0.2を超える部分にピンクのマーカーを引いています。
相関係数が ′----′ となっているのは、今回のデータではサンプル数不足により有意性ある相関係数値が得られなかった
(t 検定の p値が 0.1を超えている)部分です。
表5-2. 直近3場所1勝率別の相関係数
| 直近3場所勝率 | S級戦 | A12班戦 | チャレンジ戦 | ガールズ戦 |
|---|---|---|---|---|
| 全体 | 0.074 (7,844) | 0.080 (8,194) | 0.083 (7,612) | 0.075 (3,008) |
| 30%以上 | 0.167 (1,048) | 0.075 (1,986) | 0.108 (1,276) | 0.081 (567) |
| 40%以上 | 0.203 (368) | 0.099 (820) | 0.116 (778) | 0.134 (411) |
| 50%以上 | 0.239 (135) | 0.226 (319) | ---- (478) | 0.161 (282) |
| 60%以上 | 0.299 (44) | 0.301 (102) | ---- (274) | ---- (196) |
| 70%以上 | ---- (14) | ---- (27) | ---- (172) | ---- (151) |
今回の1年分のデータだとサンプル数(該当選手数)不足により、勝率 70%以上となる選手領域の相関係数は得られていないのですが、相関係数が得られた部分から判断すると、直近3場所の勝率が高くなるほど、「最近の調子」と「今場所成績の上振れ/下振れ」の
相関係数は高くなっていくようです。
過去レースに9車立てが含まれるS級戦では、勝率 40%以上の領域で相関係数が「やや相関がある」レベルの 0.2を超えてきます。
過去レース全てが7車立て以下となるA12班戦では、勝率 50%以上の領域で相関係数が 0.2を超えてきます。
チャレンジ戦・ガールズ戦は、今回のデータでは相関係数 0.2超えの領域は得られなかったのですが、勝率が高くなると相関係数が高くなる傾向は読み取れます。
S級戦・A12班戦ともに勝率 60%以上の選手に限定すると相関係数がほぼ 0.3となります。
5-3. 勝率 60%以上の選手に限定した予測モデル
表5-2 で、S級戦・A12班戦では「直近3場所の勝率が 60%以上の選手に限定」した場合、「最近の調子」と「今場所成績の上振れ/下振れ」の相関係数は約 0.3となりました。
ここまで高くなると「最近の調子」は「選手実力」を判定する要素の一つに加えたほうが良さそうです。
A12班戦で、直近3場所の勝率 60%越えの選手に対して、「直近4ヶ月得点」だけで「今場所得点」を予測するモデルと、「直近4ヶ月得点 と 最近の調子」で「今場所得点」を予測するモデルを回帰分析によって作ると、次のようになります。
- 予測モデル1:直近4ヶ月得点だけで今場所得点を予測
- 今場所得点 = 0.785×直近4ヶ月得点 + 20.05 (自由度調整済み決定係数(※2) rf2=0.323
- 予測モデル2:直近4ヶ月得点と最近の調子で今場所得点を予測
- 今場所得点 = 0.976×直近4ヶ月得点 + 0.646×最近の調子 + 1.21 (自由度調整済み決定係数(※2) rf2=0.355)
2つのモデルの決定係数 rf2(※2) を比較して解釈すると、「勝率 60%越えの選手については、今場所得点を直近4ヶ月得点だけで説明できるのは 32.3%だが、直近4ヶ月得点と最近の調子の2変数だと 35.5%を説明できる」です。
つまり、「予測モデル2を使うと選手実力の判定確度が 3.2%アップする」ということです。
※2 予測モデルの説明変数の数が違うので、公平な比較となるよう自由度調整済みの決定係数を使用している。
5-4.実戦での「予測モデル2」の扱い方
実際のレース予想で全選手の「最近の調子」を算出したり、「予測モデル2」の計算式を計算するのはプログラムを組まない限りとても無理です。よって、上の予測モデル2の式を実際の車券予想で使えるように、計算式ではなく具体的な数値加算に変更します。
上表のA12班戦で直近3場所勝率が 60%越えの選手の「最近の調子」の分布を調査し、平均値と、正規分布だと±2σに該当する 2.5%値および 97.5%値を求めると、
2.5%値,平均値,97.5%値 = 0.12,1.50,4.51
です。
一方、予測モデル2の「直近4ヶ月得点」に対する「最近の調子」の係数比率は、0.646 ⁄ 0.976 = 0.662 です。
2.5%値,平均値,97.5%値にそれぞれ係数 0.662 を掛けると、 0.08,0.99,2.99 になります。
つまり、「選手実力=直近4ヶ月得点」とする場合、直近3場所の勝率が 60%を超える選手については、それ以前の直近4ヶ月成績と比較して調子上向きの度合いを判断し、 0.1点 ~ 3.0点 の加点 をすれば良いようです。
「過去成績を見た感じ調子下向きか上向きか」の判断も面倒であれば、一律で 1.0点 の加点 でも良いと思われます。

6. まとめ
以上の分析結果をまとめると、直近4ヶ月得点および最近の調子で選手実力を判定する方法と、判定した選手実力が実際の今場所成績に反映される度合いの考え方は次のようになります。
- 選手実力の判定として直近4ヶ月得点を用いることは妥当
- 出走表の「直近4ヶ月得点」と「今場所成績」との相関係数は男子競輪で0.7前後、ガールズだと0.8越えであり、強い相関関係がある。選手実力の判定として直近4ヶ月得点を用いることは妥当である。
ただし男子競輪では、今場所成績を選手実力で決定される部分は50%未満であり、50%以上はそれ以外の要素(レース展開等)で決定される。
ガールズケイリンでは、今場所成績を選手実力で決定される部分は約70%あり、それ以外の要素(レース展開等)で決定される部分は約30%に留まる。 - 直近3場所の勝率が 60%以上となる場合、選手実力としては 直近4ヶ月得点に 0.1点 ~ 3.0点 の点数加算 が必要
- 直近3場所の勝率が 60%を超える選手は、それ以前の直近4ヶ月成績と比較して調子上向きの度合いを判断し、選手実力としては 直近4ヶ月得点に 0.1点 ~ 3.0点 の点数加算 が必要である。
「調子の上向き度合いの判断」が面倒であれば、一律で 1.0点 の加点 でも良い。
この加点により選手実力の判定確度が約3%アップする。 - 直近3場所の勝率が 60%に満たない場合、多少の直近成績の好調/不調は偶発的なものと考えて良い
- 直近3場所の勝率が 60%を満たない場合、最近の調子と今場所成績の上振れ/下振れの相関関係は小さく、選手実力の判定に直近4ヶ月得点以外の加点・減点は特に不要である。
高い勝率を伴わない好調・不調は偶発的なもので、長続きするものではないようだ。好調・不調が継続されれば、それは実力の上昇・低下ということであり、直近4ヶ月得点に反映される。
補足1)今回は直近4ヶ月にクラス変更を伴う「昇降級班」がなかった選手が調査対象です。
「昇降級班」があった選手については、2020年の分析記事「昇格・降格選手の正しい実力判定法」を参照ください。
補足2)直近4ヶ月得点のかわりにGamboo予想ページで提供しているG指数を用いると、新人選手や長欠明け選手の実力判定もでき、より的確な選手実力の判定が可能となります。(2019年の分析記事「G指数を徹底検証」を参照)