遠山競輪研究所

昇格・降格選手の正しい実力判定法( 2020/12/21 )
競輪では、前期(1~6月)・後期(7~12月)の期変わり時に選手の級班変更が行なわれます。
従って、各期の初頭(1月および7月)では昇級・降級・昇班・降班した選手が多数いて、レース予想が難しくなります。
例えば期初頭のA級1・2班戦のレースで「S級から降級してきた選手」「前の期もA級1・2班だった選手」「A級3班から昇班してきた選手」が混在すると、
出走表に記載される各選手の直近4ヶ月の平均競走得点(=前期の最終3ヶ月間の平均競走得点)では素直に実力比較できません。
今回は昨年の期変わり(2019年後期⇒2020年前期)直後のレース結果を調査し、競走得点の補正による昇格・降格選手の実力の判定法を求めたいと思います。
Gambooで推奨しているG指数は各クラスのレースのレベル差を考慮した得点計算となっているので、級班変更のあるなしに関係なくある程度正しく実力判定できますが、それでも勢いある若手選手の昇班・昇級直後の実力把握には若干の補正が必要となります。
G指数における昇格・降格選手の実力判定法についても一緒に検討します。
1. 昇格・降格選手の競走得点補正
2019年後期から2020年前期の期変わりにおいて、「A級1・2班⇔S級」,「A級3班⇔A級1・2班」の昇級・降級・昇班・降班があった選手について、昇降級班前の2019年10月~12月の3ヶ月間で得た競走得点と、昇降級班直後に初参戦した開催で得た競走得点の関係を調査しました。
その結果から、昇格・降格選手の過去成績の競走得点に補正を行なって適正値を算出し、従来難しかった昇格・降格選手の実力の判定方法を導きます。
(直近の期変わりは2020年前期⇒2020年後期なのですが、今年は新型コロナ流行の影響で期変わりのタイミングでG3以下のレースが全て7車立て制になったので、昇格・降格前後の成績について同じ条件下での比較ができませんでした。よって1年前の期変わりデータを用いました。)
1-1. 「A級1・2班⇒S級」昇級選手の競走得点
昨年の期変わり(2019年後期⇒2020年前期)に、A級1・2班からS級2班へ定期昇級した選手について、昇級前3ヶ月間(2019年10月~12月)の平均競走得点(※1)と、昇級後2020年1月に初出走した開催で得た平均競走得点の関係をプロットした散布図です。
※1:「昇級前3ヶ月の平均競走得点」は、昇級後1月に初出走時の出走表に記載される「直近4ヶ月の平均競走得点」と同じものです。
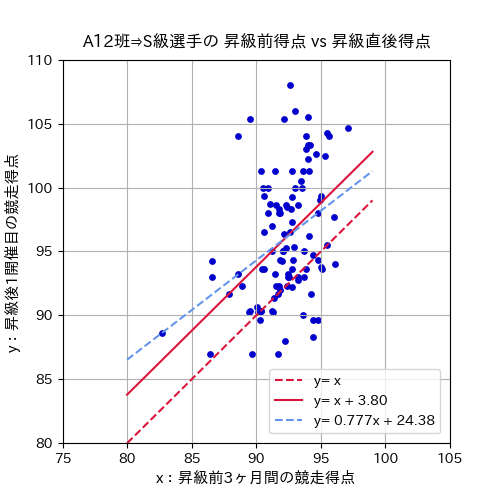
昇級直前のA級1・2班戦での競走得点が昇級後のS級戦でもその選手の実力を示す値であれば、その分布は図の赤破線「 \(y=x\) 」を中心とした分布であるはずですが、実際の成績はそれより上方に分布しています。
つまり、A級1・2班⇒S級に昇級した選手について、競走得点を用いて他選手との実力比較する場合は、\(+α\) する必要があります。
期変わり直後の成績を \(y=x+α\) とした場合に、最小二乗法で最適な \(α\) 値を求めると、競走得点の補正式は「 \(y=x+3.80\) 」(図内の赤実線)となります。
なお昇級後2開催目以降になると、出走表の直近4ヶ月競走得点の中に昇級後のレースが混ざってくるので、 \(α\) 値をレース数の比率で修正します。
直近4ヶ月の全レース数を \(n0\) 、うち昇級前レース数を \(n1\) とした場合、1開催目も含めて 昇級後の競走得点補正式は次のようになります。
A級1・2班⇒S級 昇級選手の補正競走得点
\[~~y=x~+(3.80×n1/n0)\tag{1-1}\]- \(y\)
- 補正競走得点(真の実力値)
- \(x\)
- 直近4ヶ月の競走得点
- \(n0\)
- 直近4ヶ月の全レース数
- \(n1\)
- うち昇級前のレース数
この補正を行なうことで前期もS級だった選手の競走得点と平等に点数比較が行えます。
ちなみに回帰分析によって関係式を求めると、図内の水色破線である「 \(y=0.777x+24.38\) 」となります。
こちらのほうが総合的な誤差は小さいのですが、計算が面倒(得に昇級後2場所目以降)ですので、単純な加算で計算可能な(1-1)式を採用します。
1-2. 「S級⇒A級1・2班」降級選手の競走得点
同様に昨年の期変わり時に、S級からA級1・2班へ降級した選手の競走得点の散布図です。
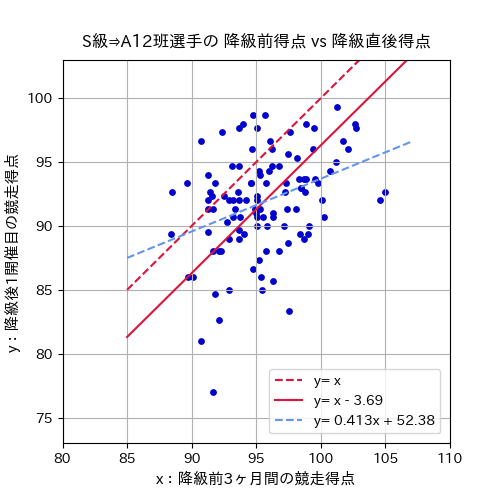
降級前の競走得点が降級後のA級1・2班戦でもその選手の実力を示す値であれば、その分布は図の赤破線「 \(y=x\) 」を中心とした分布であるはずですが、実際の成績はそれより下方に分布しています。
つまり、S級⇒A級1・2班に降級した選手について、競走得点を用いて他選手との実力比較する場合は、\(-α\) する必要があります。
最小二乗法で最適な \(α\) 値を求めると、競走得点の補正式は「 \(y=x-3.69\) 」(図内の赤実線)となります。
降級後2開催目以降にも対応可能なように、出走表の直近4ヶ月のレース数の比率で \(α\) 値に修正をかけると、降級後の競走得点補正式は次のようになります。
S級⇒A級1・2班 降級選手の補正競走得点
\[~~y=x~-(3.69×n1/n0)\tag{1-2}\]- \(y\)
- 補正競走得点(真の実力値)
- \(x\)
- 直近4ヶ月の競走得点
- \(n0\)
- 直近4ヶ月の全レース数
- \(n1\)
- うち降級前のレース数
この補正を行なうことで前期もA級1・2班だった選手の競走得点と平等に点数比較が行えます。
ちなみに回帰分析によって関係式を求めると、図内の水色破線である「 \(y=0.413x+52.38\) 」となりますが、前述したように単純な加算で計算可能な(1-2)式を採用します。
1-3. 「A級3班⇒A級1・2班」昇班選手の競走得点
同様に昨年の期変わり時に、A級3班からA級1・2班へ昇班した選手の競走得点の散布図です。
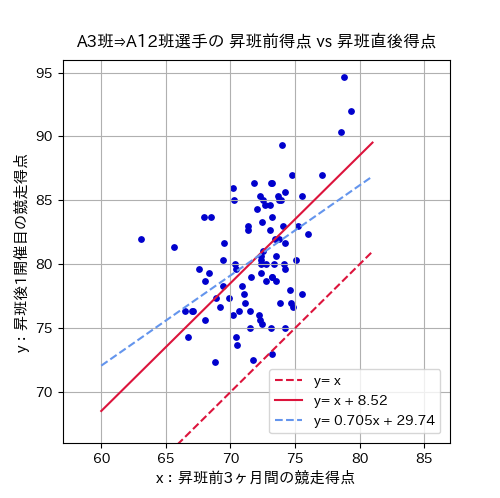
昇班前の競走得点が昇班後のA級1・2班戦でもその選手の実力を示す値であれば、その分布は図の赤破線「 \(y=x\) 」を中心とした分布であるはずですが、実際には殆どの選手の実績が赤破線より上方に分布しています。
つまり、A級3班⇒A級1・2班に昇班した選手について、競走得点を用いて他選手との実力比較する場合は、\(+α\) する必要があり、その値は大きいようです。
最小二乗法で最適な \(α\) 値を求めると、競走得点の補正式は「 \(y=x+8.52\) 」(図内の赤実線)となります。
昇班後2開催目以降にも対応可能なように、出走表の直近4ヶ月のレース数の比率で \(+α\) 値に修正をかけると、昇班後の競走得点補正式は次のようになります。
A級3班⇒A級1・2班 昇班選手の補正競走得点
\[~~y=x~+(8.52×n1/n0)\tag{1-3}\]- \(y\)
- 補正競走得点(真の実力値)
- \(x\)
- 直近4ヶ月の競走得点
- \(n0\)
- 直近4ヶ月の全レース数
- \(n1\)
- うち昇班前のレース数
この補正を行なうことで前期もA級1・2班だった選手の競走得点と平等に点数比較が行えます。
ちなみに回帰分析によって関係式を求めると、図内の水色破線である「 \(y=0.705x+29.74\) 」となります。
1-4. 「A級1・2班⇒A級3班」降班選手の競走得点
同様に昨年の期変わり時に、A級1・2班からA級3へ降班した選手の競走得点の散布図です。
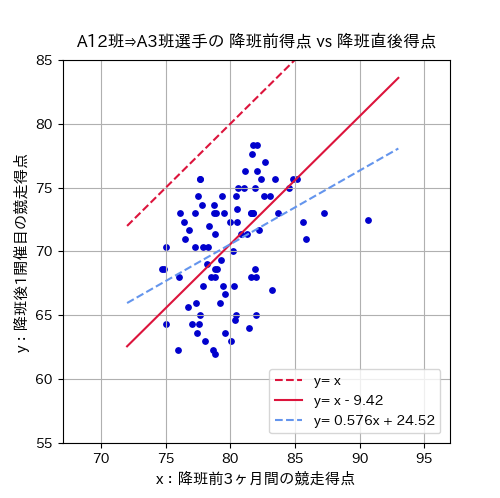
降班前の競走得点が降班後のA3班戦でもその選手の実力を示す値であれば、その分布は図の赤破線「 \(y=x\) 」を中心とした分布であるはずですが、実際には全選手の実績が赤破線より下方に分布しています。
つまり、A級1・2班⇒A級3班に降班した選手について、競走得点を用いて他選手との実力比較する場合は、\(-α\) する必要があり、その値は大きいようです。
最小二乗法で最適な \(α\) 値を求めると、競走得点の補正式は「 \(y=x-9.42\) 」(図内の赤実線)となります。
降班後2開催目以降にも対応可能なように、出走表の直近4ヶ月のレース数の比率で \(α\) 値に修正をかけると、昇級後の競走得点補正式は次のようになります。
A級1・2班⇒A級3班 降班選手の補正競走得点
\[~~y=x~-(9.42×n1/n0)\tag{1-4}\]- \(y\)
- 補正競走得点(真の実力値)
- \(x\)
- 直近4ヶ月の競走得点
- \(n0\)
- 直近4ヶ月の全レース数
- \(n1\)
- うち降班前のレース数
この補正を行なうことで前期もA級3班だった選手の競走得点と平等に点数比較が行えます。
ちなみに回帰分析によって関係式を求めると、図内の水色破線である「 \(y=0.576x+24.52\) 」となります。
2. G指数における補正
Gambooの予想情報で掲示しているG指数も選手の能力を示す指数であり、その的確度は平均競走得点を上回るものですが、G指数における昇格・降格選手の状況はどうなのでしょうか。検証してみます。
2-1. 「A級1・2班⇒S級」昇級選手のG指数
昨年の期変わり(2019年後期⇒2020年前期)時に、A級1・2班からS級へ昇級した選手について、昇級前7場所のG指数と、昇級後に初出走した開催で得たG指数の関係をプロットした散布図です。
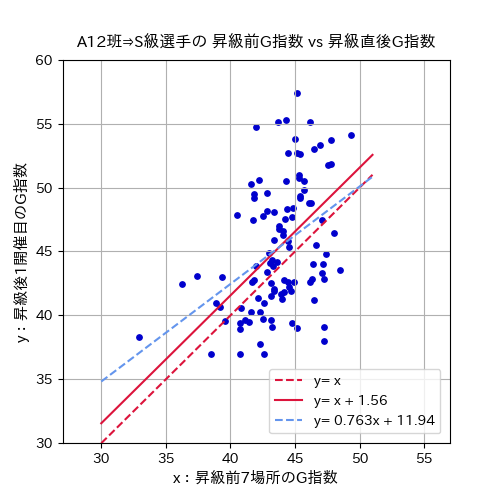
昇級前のA級1・2班戦で得たG指数が昇級後のS級戦でもその選手の実力を示すと仮定した「 \(y=x\) 」を中心とした分布となっており、競走得点に比べるとG指数は補正なしでも昇級選手の実力をある程度的確に示す指数となっています。
さらに最適な実力値指数を求めて、\(y=x+α\) と仮定した式の \(α\) 値を最小二乗法で求めると、G指数の補正式は「 \(y=x+1.56\) 」(図内の赤実線)となります。
競走得点の補正式と同様に、昇級後2開催目以降にも対応可能なように、出走表の直近4ヶ月のレース数の比率で \(α\) 値に補正をかけると、昇級後のG指数補正式は次のようになります。
A級1・2班⇒S級 昇級選手の補正G指数
\[~~y=x~+(1.56×n1/n0)\tag{2-1}\]- \(y\)
- 補正G指数(真の実力値)
- \(x\)
- 直近7場所のG指数
- \(n0\)
- 直近7場所の全レース数
- \(n1\)
- うち昇級前のレース数
この補正を行なうことで前期もS級だった選手のG指数と平等に指数比較が行えます。
ちなみに回帰分析によって関係式を求めると、図内の水色破線である「 \(y=0.763x+11.94\) 」となります。
こちらのほうが総合的な誤差は小さいのですが、計算が面倒(得に昇級後2場所目以降)ですので、単純な加算で計算可能な(2-1)式を採用します。
2-2. 「S級⇒A級1・2班」降級選手のG指数
同様に昨年の期変わり時に、S級からA級1・2班へ降級した選手のG指数の散布図です。
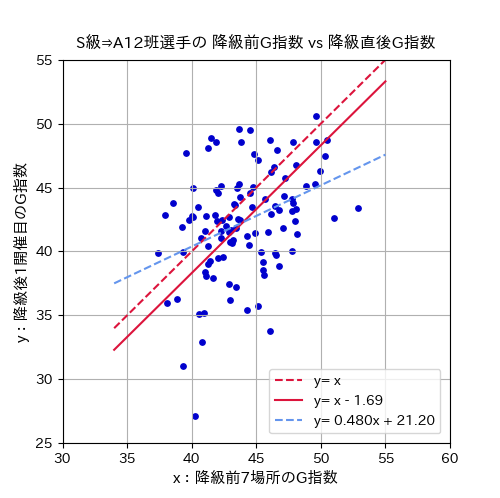
降級前のS級戦で得たG指数が降級後のA級1・2班戦でもその選手の実力を示す「 \(y=x\) 」(図内の赤破線)は分布の中心近くを通っており、競走得点に比べるとG指数は補正なしでも降級選手の実力をある程度的確に示す指数となっています。
さらに最適な実力値指数を求めて、\(y=x+α\) と仮定した式の \(α\) 値を最小二乗法で求めると、G指数の補正式は「 \(y=x-1.69\) 」(図内の赤実線)となります。
降級後2開催目以降にも対応可能なように、直近7場所のレース数の比率で \(α\) 値に修正をかけると、降級後のG指数補正式は次のようになります。
S級⇒A級1・2班 降級選手の補正G指数
\[~~y=x~-(1.69×n1/n0)\tag{2-2}\]- \(y\)
- 補正G指数(真の実力値)
- \(x\)
- 直近7場所のG指数
- \(n0\)
- 直近7場所の全レース数
- \(n1\)
- うち降級前のレース数
この補正を行なうことで前期もA級1・2班だった選手のG指数と平等に指数比較が行えます。
ちなみに回帰分析によって関係式を求めると、図内の水色破線である「 \(y=0.480x+21.20\) 」となります。
こちらのほうが総合的な誤差は小さいのですが、計算が面倒(得に降級後2場所目以降)ですので、単純な加算で計算可能な(2-2)式を採用します。
2-3. 「A級3班⇒A級1・2班」昇班選手のG指数
同様に昨年の期変わり時に、A級3班からA級1・2班へ昇班した選手のG指数の散布図です。
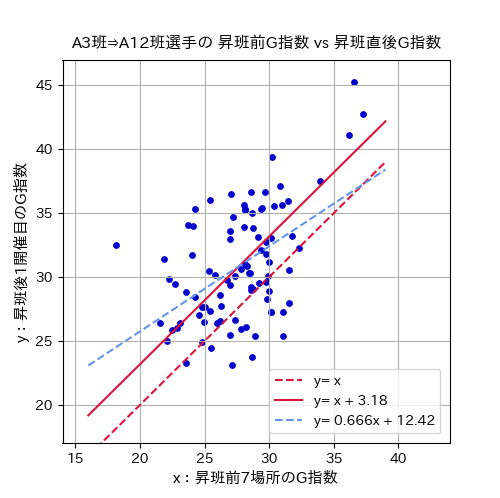
昇班前のA級1・2班戦で得たG指数が昇班後のS級戦でもその選手の実力を示す「 \(y=x\) 」(図内の赤破線)は分布の中心より下側を通っており、的確に実力を示す指数とするには \(+α\) の補正を行ったほうが良さそうです。
最小二乗法で最適な \(α\) 値を求めると、競走得点の補正式は「 \(y=x+3.18\) 」(図内の赤実線)となります。
昇班後2開催目以降にも対応可能なように、出走表の直近7場所のレース数の比率で \(α\) 値に修正をかけると、昇班後のG指数補正式は次のようになります。
A級3班⇒A級1・2班 昇班選手の補正G指数
\[~~y=x~+(3.18×n1/n0)\tag{2-3}\]- \(y\)
- 補正G指数(真の実力値)
- \(x\)
- 直近7場所のG指数
- \(n0\)
- 直近7場所の全レース数
- \(n1\)
- うち昇班前のレース数
この補正を行なうことで前期もA級1・2班だった選手のG指数と平等に指数比較が行えます。
ちなみに回帰分析によって関係式を求めると、図内の水色破線である「 \(y=0.666x+12.42\) 」となります。
こちらのほうが総合的な誤差は小さいのですが、計算が面倒(得に昇班後2場所目以降)ですので、単純な加算で計算可能な(2-3)式を採用します。
2-4. 「A級1・2班⇒A級3班」降班選手のG指数
同様に昨年の期変わり時に、A級1・2班からA級3班へ降班した選手のG指数の散布図です。
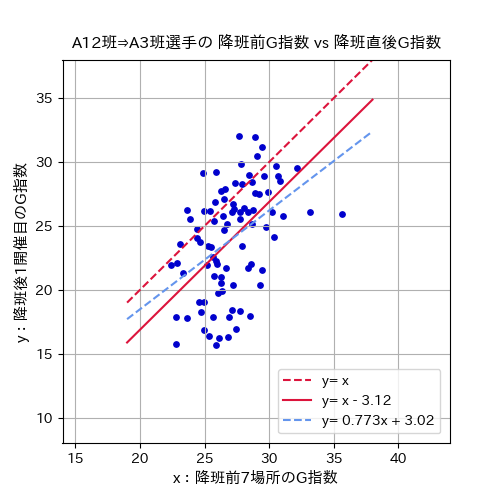
降班前のA級1・2班戦で得たG指数が降班後のA級3班戦でもその選手の実力を示す「 \(y=x\) 」(図内の赤破線)は分布の中心より上側を通っており、的確に実力を示す指数とするには \(-α\) の補正を行ったほうが良さそうです。
最小二乗法で最適な \(α\) 値を求めると、競走得点の補正式は「 \(y=x-3.12\) 」(図内の赤実線)となります。
降班後2開催目以降にも対応可能なように、出走表の直近7場所のレース数の比率で \(α\) 値に修正をかけると、降班後のG指数補正式は次のようになります。
A級1・2班⇒A級3班 降班選手の補正G指数
\[~~y=x~-(3.12×n1/n0)\tag{2-4}\]- \(y\)
- 補正G指数(真の実力値)
- \(x\)
- 直近7場所のG指数
- \(n0\)
- 直近7場所の全レース数
- \(n1\)
- うち降班前のレース数
この補正を行なうことで前期もA級3班だった選手のG指数と平等に指数比較が行えます。
ちなみに回帰分析によって関係式を求めると、図内の水色破線である「 \(y=0.773x+3.02\) 」となります。
こちらのほうが総合的な誤差は小さいのですが、計算が面倒(得に降班後2場所目以降)ですので、単純な加算で計算可能な(2-4)式を採用します。
3. 補正式のまとめ
以上の補正式を表にまとめました。今後のレース予想にご利用下さい。
昇級・降級・昇班・降班選手の競走得点 及び G指数 補正式
| 級班変更 | 競走得点の補正式 | G指数の補正式 |
|---|---|---|
| A級1・2班⇒S級 | \[y=x~+(3.80×n1/n0)\tag{1-1}\] | \[y=x~+(1.56×n1/n0)\tag{2-1}\] |
| S級⇒A級1・2班 | \[y=x~-(3.69×n1/n0)\tag{1-2}\] | \[y=x~-(1.69×n1/n0)\tag{2-2}\] |
| A級3班⇒A級1・2班 | \[y=x~+(8.52×n1/n0)\tag{1-3}\] | \[y=x~+(3.18×n1/n0)\tag{2-3}\] |
| A級1・2班⇒A級3班 | \[y=x~-(9.42×n1/n0)\tag{1-4}\] | \[y=x~-(3.12×n1/n0)\tag{2-4}\] |
| 式の記号 | \(~y\):補正競走得点(真の実力値 | \(~y\):補正G指数(真の実力値) |
| \(~x\):直近4ヶ月の競走得点 | \(~x\):直近7場所のG指数 | |
| \(n0\):直近4ヶ月の全レース数 | \(n0\):直近7場所の全レース数 | |
| n1:うち級班変更前のレース数 | \(n1\):うち級班変更前のレース数 |