遠山競輪研究所

バック取得ラインを予測する( 2020/07/16 )
購入車券を決定するうえで「どのラインがバックを取るか」の想定は大変重要です。
今回はバック取得ラインを予測する方法について検討しました。
まずはバック取得したラインの成績を集計してその有利さを確認し、次にバック取得に関係する要素は何かを調べ、「バック取得確率の計算式」を作成してバック取得するラインの予測実験を行いました。
1. バック取得ラインの成績
まずラインの定義ですが、ここでは2車以上で連携してチームを組んで走ることをラインとします。
直近3年間(2017年5月~2020年4月)のレースで、バック取得したラインの成績を以下にまとめました。
表1-1.はライン先頭選手の、表1-2.は番手選手の勝率・連対率です。
表1-1. バック取得したライン先頭選手の勝率・連対率
| クラス・車立て数 | 33バンク | 400バンク | 500バンク | 全場 | |
|---|---|---|---|---|---|
| S級戦 9車立て | 勝率 連対率 | 27.58% 49.49% | 19.72% 38.30% | 18.28% 33.46% | 20.97% 39.89% |
| A12班戦 9車立て | 勝率 連対率 | 32.85% 54.14% | 24.57% 42.99% | 17.36% 33.43% | 25.46% 44.20% |
| A12班戦 7車立て | 勝率 連対率 | 39.85% 62.60% | 30.48% 52.22% | 26.83% 46.33% | 31.61% 53.27% |
| チャレンジ 7車立て | 勝率 連対率 | 52.82% 72.67% | 44.68% 65.07% | 44.29% 63.96% | 45.98% 66.21% |
| 全クラス計 | 勝率 連対率 | 36.85% 58.15% | 28.73% 48.05% | 26.54% 43.94% | 29.93% 49.43% |
表1-2. バック取得したライン番手選手の勝率・連対率
| クラス・車立て数 | 33バンク | 400バンク | 500バンク | 全場 | |
|---|---|---|---|---|---|
| S級戦 9車立て | 勝率 連対率 | 26.00% 50.97% | 28.30% 50.05% | 24.97% 44.79% | 27.68% 49.85% |
| A12班戦 9車立て | 勝率 連対率 | 25.17% 51.02% | 25.33% 48.63% | 22.84% 44.85% | 25.12% 48.76% |
| A12班戦 7車立て | 勝率 連対率 | 25.84% 57.46% | 25.58% 52.77% | 22.78% 48.65% | 25.31% 53.09% |
| チャレンジ 7車立て | 勝率 連対率 | 17.22% 50.31% | 17.80% 47.59% | 17.47% 46.26% | 17.68% 47.91% |
| 全クラス計 | 勝率 連対率 | 23.64% 51.58% | 24.37% 49.26% | 21.85% 45.83% | 24.04% 49.37% |
全選手平均の勝率・連対率は9車立てで 11.1%・22.2%(=1/9・2/9)、7車立てで 14.3%・28.6%(=1/7・2/7)ですが、上表の勝率・連対率はこれを大きく上回っており、バック取得ラインの先頭選手、番手選手の成績はとても高いことがわかります。
他にも次のことが言えるようです。
- ・S級戦およびA12班戦の9車立てでは、概ね「先頭選手の成績 < 番手選手の成績」(33バンクを除く)。
- ・A12班戦7車立ておよびチャレンジ戦では、概ね「先頭選手の成績 > 番手選手の成績」(A12班戦の400・500バンクの連対率を除く)。
- ・チャレンジ戦におけるバック取得したライン先頭選手の勝率・連対率は特に高く、全場平均で「45%越え・66%越え」となる。
- ・周長が短いバンクのほうが長いバンクよりバック取得ラインの成績は高い。
- ・特にライン先頭選手では、短走路の成績と長走路の成績の差が大きい。
2. バック取得に関係する予想要素
バックを取得したラインの先頭および番手選手の勝率・連対率は相当高いことがわかりました。
購入車券を検討するうえで、「どのラインがバックを取るか」の想定は大変重要です。
ではどのような予想要素(予想ファクター)がラインのバック取得に関係するのでしょうか?
2-1. ライン先頭選手の直近7場所バック数と、レースでのバック取得との関係
まず最初に思いつくのは、ライン先頭選手の「過去成績におけるバック数」でしょう。
ここでは過去成績におけるバック数として「直近7場所バック数」を次のように定義し、実際のレースでのバック取得との関係を調べてみました。
- 直近7場所バック数
- 過去成績の直近7場所のバック数を21走換算した数値。
例えば、直近7場所の出走レース数が18でバック数が8だった場合、
8 / 18 x 21 = 9.3 と計算して、9.3を直近7場所バック数とする。
直近3年間(2017年5月~2020年4月)のレースから S級戦の3分戦を抽出し、「ライン先頭選手の直近7場所バック回数」と「実レースでのバック取得の有無」のデータを作成しました。
表2-1. S級戦の3分戦:バック取得データ
| レース日 | 場番号 | レース 番号 | 車番 | 直近7場所 バック数 | バック取得の 有無 |
| 2017/5/1 | 38 | 6 | 2 | 0.8 | 0 |
| 2017/5/1 | 38 | 6 | 3 | 2.7 | 0 |
| 2017/5/1 | 38 | 6 | 4 | 5.9 | 1 |
| 2017/5/1 | 38 | 10 | 5 | 6.5 | 0 |
| 2017/5/1 | 38 | 10 | 8 | 10.5 | 1 |
| 2017/5/1 | 38 | 10 | 3 | 3.7 | 0 |
| ... | ... | ... | ... | ... | ... |
このデータを直近過去7場所バック数別に「選手の数」と「バック取得の数」を集計し、バック取得率を算出してグラフ化すると下図となります。
図中の赤い線から分かるように、ライン先頭選手の「直近7場所バック数」とそのラインが「バック取得する確率」の間には明らかに相関関係があるようです。
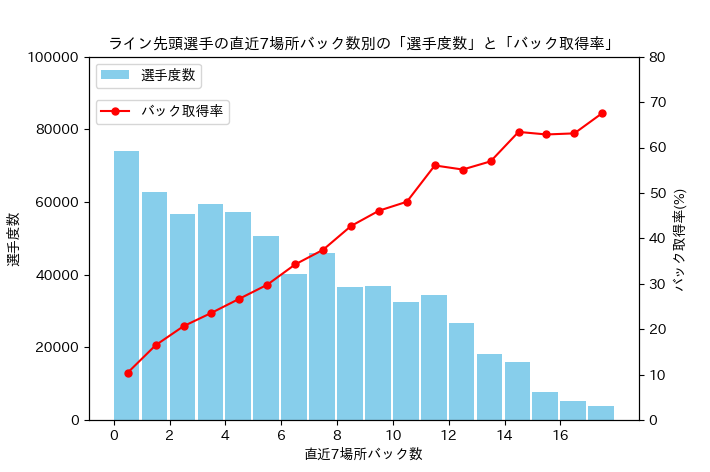
表2-1 のデータを、バックを取得した場合と取得しなかった場合に分けて ライン先頭選手の「直近7場所バック数」を集計し、相関比を算出したのが次の表です。
表2-2. 「ライン先頭選手の直近7場所バック回数」と「バック取得」の相関比
| 予想要素 | 全体 | バック取得した | バック取得せず | 相関比 | ||||
|---|---|---|---|---|---|---|---|---|
| データ範囲 | 平均値 | 標準偏差 | 平均値 | 標準偏差 | 平均値 | 標準偏差 | ||
| ライン先頭選手の 直近7場所バック数 | 0.0 ~ 21.0 | 6.09 | 4.31 | 8.13 | 4.27 | 5.08 | 3.97 | 0.111 |
相関比とは2変数間の相関の強さを表す指数で 0 から 1 までの値を取り、1 に近いほうが相関が強いことを意味します。
上表の相関比 0.111 という数値は、強くはないが一応2変数間に「相関関係がある」と言って良いレベルです。
2-2. その他の予想要素とバック取得との関係
その他の「ラインのバック取得」に関係しそうな予想要素を洗い出し、実際のバック取得との関係を調べてみます。
下の表2-3 および表2-4 の数値は、直近3年間(2017年5月~2020年4月)のS級戦のライン3分戦レースで調べた値です。
・量的データの予想要素
前述の直近7場所バック数など、数量として測定できるデータ(量的データ)の場合は、相関比を算出してバック取得との関係を調べました。
相関比は2変数間の相関の強さを表す統計量で、今回の「バック取得したか否か」のように片方の変数がカテゴリーデータの場合に使用します。
やはり「直近7場所バック数」が最も相関比が高く、次が「直近7場所ホーム数」でした。
「ラインの長さ」は思っていたほどバック取得の大きな要因ではありませんでした。
「先頭選手のG指数値」はバック取得との関係は殆ど無いのですが、「番手選手のG指数値」はある程度関係しているようです。
表2-3. 量的データの予想要素と「バック取得」との関係
| 予想要素 | 全体 | バック取得した | バック取得せず | 相関比 | ||||
|---|---|---|---|---|---|---|---|---|
| データ範囲 | 平均値 | 標準偏差 | 平均値 | 標準偏差 | 平均値 | 標準偏差 | ||
| 先頭選手の直近7場所バック数 | 0.0 ~ 21.0 | 6.09 | 4.31 | 8.13 | 4.27 | 5.08 | 3.97 | 0.111 |
| 先頭選手の直近7場所ホーム数 | 0.0 ~ 20.1 | 6.03 | 4.33 | 7.98 | 4.31 | 5.08 | 4.01 | 0.099 |
| ラインの長さ | 2 ~ 5 | 2.75 | 0.49 | 2.89 | 0.44 | 2.69 | 0.50 | 0.038 |
| 先頭選手のG指数値(注) | -19.93 ~ 22.19 | 1.18 | 4.40 | 1.62 | 4.63 | 0.97 | 4.27 | 0.005 |
| 番手選手のG指数値(注) | -14.57 ~ 17.58 | 1.64 | 3.84 | 2.48 | 3.89 | 1.22 | 3.75 | 0.024 |
- (注) 先頭選手のG指数値、番手選手のG指数値
- ここでのG指数値は、出走メンバーのG指数の中央値との差とする。
例えば、9車立てレースの場合、高いほうから5番目の選手のG指数が中央値であり、ライン先頭(番手)選手のG指数が中央値より5.2点高かった場合、ライン先頭(番手)選手のG指数値は 5.2。
・カテゴリーデータの予想要素
予想要素がカテゴリーデータ(「該当」か「該当じゃない」かの2値)の場合は、オッズ比を算出してバック取得との関係を調べました。
例えば 下表の「ライン先頭と番手が同県」については、同県の場合のバック取得オッズは 2,368 / 4,677=0.51、非同県の場合のバック取得オッズは 8,045 / 16,566=0.49 であり、この比がオッズ比 0.51 / 0.49=1.04 です。
オッズ比は0~∞ の値を取り、1に近い場合は両オッズに差がなく、1より小さいか 1より大きい場合には両オッズに差がある、つまり「予想要素はラインのバック取得に影響を与える」と判断します。
下表のオッズ比から判断すると、バック取得に影響を与える予想要素は「ライン先頭より番手が年上」だけのようです。
表2-4. カテゴリーデータの予想要素と「バック取得」との関係
| 予想要素 | 全体 | バック取得/非取得での分割表 | オッズ比 (信頼区間95%) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| カテゴリ1 | 度数 (比率) | カテゴリ2 | 度数 (比率) | カテゴリ | B取得 | 非取得 | オッズ | ||
| ライン先頭と 番手が同県 | 同県 | 7,045 (22%) | 非同県 | 24,611 (78%) | 同県 | 2,368 | 4,677 | 0.51 | 1.04 0.99 ~ 1.10 |
| 非同県 | 8,045 | 16,566 | 0.49 | ||||||
| ライン先頭と 番手が同地区 | 同地区 | 24,161 (76%) | 非同地区 | 7,495 (24%) | 同地区 | 7,856 | 16,305 | 0.48 | 0.93 0.88 ~ 0.98 |
| 非同地区 | 2,557 | 4,938 | 0.52 | ||||||
| ライン先頭より 番手が年上 | 年上 | 27,180 (86%) | 年下 (同年含) | 4,476 (14%) | 年上 | 9,246 | 17,934 | 0.52 | 1.46 1.36 ~ 1.57 |
| 年下・同 | 1,167 | 3,309 | 0.35 | ||||||
- 表内の数値説明
- 例えば 上表の「ライン先頭と番手が同県」については、直近3年間のS級戦の3分戦で、「ラインの先頭と番手が同県だったケースが7,045件、非同県だったケースが24,611件で、同県のうち2,368件でそのラインがバック取得し 4,677件がバック取得せず、非同県のうち8,045件がバック取得し 16,566件がバック取得せず」を表わしている。
3. バック取得ラインの予測
3-1. ロジスティック回帰分析
今回のように、「対象のラインがバック取得するか否か」というように目的変数が2値である場合の予測には、近年「ロジスティック回帰分析」という手法が良く用いられます。
という式を用いて予測する方法で、説明変数 \(x\) を変化させた場合 \(p\) は 0から1の範囲で変化します。得られる \(p\) は目的変数(1 or 0)が1となる確率です。
(3-1)式の \(a_{1},a_{2},…,a_{n}\) および \(b\) のパラメータを求める手法の説明はここでは省略します。
今回は最尤法という手法で解いているpython のScikit-learnライブラリを用いて分析を行いました。
表2-1.のデータを用いて、「ライン先頭選手の直近7場所バック数」を説明変数に、「ラインのバック取得の有無」を目的変数に設定して1変数(3-1式の\(x\)変数は\(x_{1}\)のみ)でのロジスティック回帰分析を行うと、
\(a_{1}\)= 0.171 \(b\)= -1.829
が求まりました。このパラメータを用いて \(p\) の変化部分をプロットしました。(3-1)式が表現するロジスティック曲線のイメージが分かると思います。(実際の直近7場所バック数が取り得る値は 0~21です)
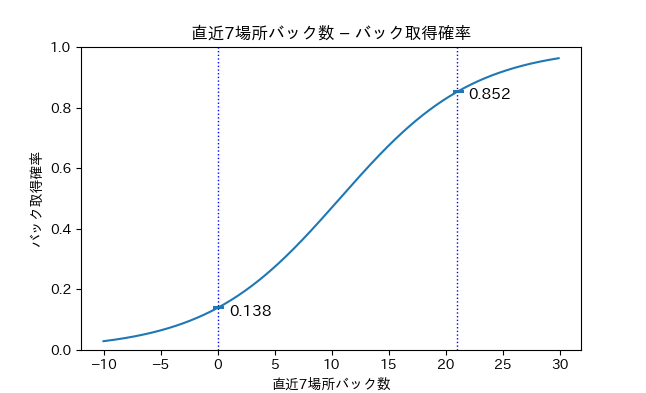
3-2. バック取得確率の計算式
では、表2-3 および表2-4 から得られたラインのバック取得に関係している予想要素、
1. 先頭選手の直近7場所バック数
2. 先頭選手の直近7場所ホーム数
3. ラインの長さ
4. ライン番手選手のG指数値
5. ライン先頭選手より番手選手が年上か否か
を説明変数\(x_{1}\)~\(x_{5}\)としてロジスティック回帰分析で「バック取得確率の計算式」を作成します。
なお、今回は準備した直近3年間のレースデータを「学習用」と「テスト用」に分けて、学習用データで式を作成し、テスト用データで予測を行って、実結果との比較で予測式の精度確認までを行います。
- 準備データ: 2017年5月~2020年4月の3年間内に開催されたS級戦のライン3分戦レース。
- 学習用 : 上の準備データのうち、開催日が「3の倍数」または「3の倍数+1」のレース。(7,086個)
- テスト用: 上の準備データのうち、開催日が「3の倍数+2」のレース。(3,466個)
学習用データでロジスティック回帰分析によって求めたバック取得確率の計算式は次のとおりです。
- \(Pbk\):ラインがバックを取得する確率
- \(x_{1}\) : ライン先頭選手の直近7場所バック数(21走当りに換算した数値)
- \(x_{2}\) : ライン先頭選手の直近7場所ホーム数(21走当りに換算した数値)
- \(x_{3}\) : ライン長(ラインを構成する人数)
- \(x_{4}\) : ライン番手選手のG指数値(中央値からの点数差)
- \(x_{5}\) : ライン先頭選手より番手選手が年上か否か(1 or 0)
3-3. バック取得ラインの予測と的中率
実際のS級戦の3分戦で「どのラインがバックを取るか」を予測するには、 「3ラインのバック取得確率を求め、最も確率が高いラインがバックを取得する」と判断することになります。
準備したテスト用データで「どのラインがバックを取るか」を予測実験しました。
結果は次のとおりでした。
| 予測レース数 | 有効レース数 | 的中数 | 的中率 | 確率均衡数 | 準的中率 |
|---|---|---|---|---|---|
| 3,466 | 3,442 | 1,952 | 56.7% | 312(9.0%) | 60.4% |
- 有効レース数
- 予測を行ったレースでラインに属さない単騎選手がバック取得したレースが24個あり、これを除いたものを有効レースとした。
- 的中数・的中率
- 予測したラインが実際にバック取得したレース数およびその比率。
- 確率均衡数
- バック取得確率が上位2ラインで均衡(差が5%未満)しているレースの数。()内は全体に対する比率。
- 準的中率
- 上位2ラインの確率が均衡したレースではその両方を候補とし、どちらかがバック取得したら的中とカウントした場合の的中率。
テスト用データ全体で実際にバック取得したラインと一致した的中率は56.7%となりました。(準的中率を適用しても60.4%)
3分戦なのでランダムにバック取得ラインを選択した場合は33.3%(=1/3)なので、それより23%程はアップしましたが、あまり精度良い予測とはなりませんでした。
今回はロジスティック回帰分析という統計的手法を使ってバック取得確率の計算式を作成しましたが、それ程高い的中率は得られませんでした。
実際には競輪歴が長い方だと、先頭選手のバック数に関係なく「このレースでは二段駆けとなる」等の判断もされていると思います。
予測式も二段駆けパターンを判断できるようになると、もっと高い的中率が得られるかも知れません。
今後機会があれば、そのようなことを盛り込んだ検討もしてみたいと思います。
4. A12班戦・チャレンジ戦での予測
上述と同様の手順で A12班戦、チャレンジ戦の3分戦でも バック取得確率の計算式を作成して予測を行ってみました。
表4-1 ,表4-2 は各クラスでの予想要素とバック取得との相関比およびオッズ比をまとめたものです。
表4-1. クラス別の予想要素とバック取得との相関比
| 予想要素 | S級戦 | A12班戦 9車立 | A12班戦 7車立 | チャレン ジ戦 |
|---|---|---|---|---|
| 先頭の直近7場所バック数 | 0.111 | 0.120 | 0.140 | 0.145 |
| 先頭の直近7場所ホーム数 | 0.099 | 0.106 | 0.132 | 0.109 |
| ラインの長さ | 0.038 | 0.052 | 0.073 | 0.093 |
| 先頭選手のG指数値 | 0.005 | 0.017 | 0.018 | 0.102 |
| 番手選手のG指数値 | 0.024 | 0.025 | 0.040 | 0.034 |
表4-2. クラス別の予想要素とバック取得とのオッズ比
| 予想要素 | S級戦 | A12班戦 9車立 | A12班戦 7車立 | チャレン ジ戦 |
|---|---|---|---|---|
| ライン先頭と 番手が同県 | 1.04 | 0.92 | 0.94 | 0.92 |
| ライン先頭と 番手が同地区 | 0.93 | 0.89 | 0.79 | 0.83 |
| ライン先頭より 番手が年上 | 1.46 | 1.39 | 1.50 | 1.65 |
表4-1 で特筆すべきは、チャレンジ戦では「ライン先頭選手のG指数値」と「バック取得」との相関比が大きいことです。
それを受け、チャレンジ戦の計算式において「ライン先頭選手のG指数値」を説明変数に取り入れ、「番手選手のG指数値」を説明変数から削除しました。
ロジスティック回帰分析で求めたバック取得確率の計算式は次のとおりです。
◆ 9車立てレース \[Pbk=\frac{1}{1+exp(-(0.111x_{1}+0.047x_{2}+0.671x_{3}+0.053x_{4}-0.051x_{5}-3.764))}\tag{4-1}\]
◆ 7車立てレース \[Pbk=\frac{1}{1+exp(-(0.110x_{1}+0.064x_{2}+0.815x_{3}+0.067x_{4}+0.046x_{5}-3.784))}\tag{4-2}\]
- \(Pbk\):ラインがバックを取得する確率
- \(x_{1}\) : ライン先頭選手の直近7場所バック数(21走当りに換算した数値)
- \(x_{2}\) : ライン先頭選手の直近7場所ホーム数(21走当りに換算した数値)
- \(x_{3}\) : ライン長(ラインを構成する人数)
- \(x_{4}\) : ライン番手選手のG指数値(中央値からの点数差)
- \(x_{5}\) : ライン先頭選手より番手選手が年上か否か(1 or 0)
- \(Pbk\):ラインがバックを取得する確率
- \(x_{1}\) : ライン先頭選手の直近7場所バック数(21走当りに換算した数値)
- \(x_{2}\) : ライン先頭選手の直近7場所ホーム数(21走当りに換算した数値)
- \(x_{3}\) : ライン長(ラインを構成する人数)
- \(x_{4}\) : ライン先頭選手のG指数値(中央値からの点数差)
- \(x_{5}\) : ライン先頭選手より番手選手が年上か否か(1 or 0)
予測実験をした結果は次のとおりです。
| クラス | 予測レース数 | 有効レース数 | 的中数 | 的中率 | 予想均衡数 | 準的中率 |
|---|---|---|---|---|---|---|
| A12班9車立て戦 | 5,290 | 5,248 | 3,062 | 58.3% | 519 | 61.8% |
| A12班7車立て戦 | 1,431 | 1,424 | 861 | 60.5% | 102 | 63.4% |
| チャレンジ戦 | 2,346 | 2,332 | 1,444 | 61.9% | 155 | 65.1% |
A12班戦、チャレンジ戦ではS級戦より的中率が高くなりました。
特に新人選手がデビューするチャレンジ戦ではラインの力差があるレースも多いですし、S級戦以外では二段駆けのパターンが少ないというのもその理由でしょう。