遠山競輪研究所

【111期生在校成績とデビュー期成績の関係調査】( 2018/06/29 )
昨年7月にデビューした 111期生のデータを分析して、競輪学校時の在校成績 と デビュー後7場所の成績 の関係について調べてみます。
111期生の競輪学校時の在校成績と、デビュー後7場所の実績(競走得点)を下の表1-1. にまとめました。
(表中の "昇班" にはデビュー後7場所間の特別昇班の有無を記載しています。)
表1-1. 111期生在校成績とデビュー後7場所の成績
| 氏 名 |
|---|
| 皿屋 豊 |
| 浜田 翔平 |
| 寺沼 将彦 |
| 山口 龍也 |
| 藤原 俊太郎 |
| 照屋 将貴 |
| 川口 雄太 |
| 三浦 大輝 |
| 山本 隼人 |
| 中野 真吾 |
| 小森 貴大 |
| 門脇 翼 |
| 栗田 万生 |
| 今野 大輔 |
| 菱沼 元樹 |
| 今岡 徹二 |
| 川越 勇星 |
| 菊池 竣太朗 |
| 林 慶次郎 |
| 坂本 拓也 |
| 出澤 拓也 |
| 境 啓亨 |
| 小林 裕一朗 |
| 下岡 将也 |
| 吉田 智哉 |
| 野口 裕史 |
| 猪野 泰介 |
| 山崎 賢人 |
| 戸塚 涼介 |
| 久保田 泰弘 |
| 今村 麟太郎 |
| 望月 一成 |
| 布居 大地 |
| 染谷 幸喜 |
| 田尾 駿介 |
| 吉川 希望 |
| 船瀬 惇平 |
| 門田 凌 |
| 牧田 賢也 |
| 平尾 一晃 |
| 森川 康輔 |
| 能代 谷元 |
| 大中 拓磨 |
| 高橋 大輝 |
| 中野 雄喜 |
| 谷口 幸司 |
| 白濱 一平 |
| 格清 洋介 |
| 蕗澤 鴻太郎 |
| 島村 匠 |
| 南 潤 |
| 鮫島 康治 |
| 内田 淳 |
| 桜井 大地 |
| 松本 貴治 |
| 奥村 諭志 |
| 鶴 良生 |
| 小川 丈太 |
| 伊藤 稔真 |
| 金ヶ江 勇気 |
| 吉田 昌司 |
| 府県 | 在 校 成 績 | デビュー後7場所 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| レース 数 |
1着 数 |
2着 数 |
BK 数 |
勝率 (%) |
連対率 (%) |
B取得率 (%) |
訓練得点 | 独走タイム | 総合点 | 競走 得点 |
昇班 | |||
| 得点 | 順位 | 200m | 400m | |||||||||||
| 三重 | 71 | 7 | 13 | 24 | 9.9 | 28.2 | 33.8 | 74.45 | 31 | 11.40 | 23.56 | 417.8 | 77.38 | |
| 大阪 | 68 | 0 | 2 | 0 | 0.0 | 2.9 | 0.0 | 70.79 | 59 | 12.03 | 25.18 | 252.0 | 63.79 | |
| 東京 | 69 | 1 | 4 | 7 | 1.5 | 7.3 | 10.1 | 71.62 | 55 | 11.53 | 23.77 | 324.6 | 73.24 | |
| 長崎 | 72 | 2 | 9 | 0 | 2.8 | 15.3 | 0.0 | 74.09 | 38 | 11.89 | 24.76 | 277.5 | 69.74 | |
| 岡山 | 67 | 8 | 10 | 17 | 11.9 | 26.9 | 25.4 | 75.85 | 17 | 11.58 | 23.89 | 380.0 | 76.38 | |
| 沖縄 | 68 | 2 | 7 | 0 | 2.9 | 13.2 | 0.0 | 73.54 | 45 | 11.41 | 23.76 | 316.0 | 76.48 | |
| 徳島 | 72 | 4 | 6 | 6 | 5.6 | 13.9 | 8.3 | 74.23 | 34 | 11.73 | 24.21 | 310.4 | 75.19 | |
| 宮城 | 72 | 2 | 4 | 3 | 2.8 | 8.3 | 4.2 | 73.29 | 48 | 11.60 | 24.31 | 304.9 | 69.57 | |
| 大阪 | 70 | 9 | 14 | 8 | 12.9 | 32.9 | 11.4 | 75.77 | 18 | 11.55 | 24.15 | 354.3 | 75.67 | |
| 佐賀 | 61 | 0 | 1 | 0 | 0.0 | 1.6 | 0.0 | 72.09 | 54 | 11.41 | 23.52 | 303.3 | 69.14 | |
| 福井 | 69 | 10 | 7 | 24 | 14.5 | 24.6 | 34.8 | 74.14 | 36 | 11.24 | 23.33 | 430.0 | 78.91 | |
| 秋田 | 68 | 18 | 16 | 2 | 26.5 | 50.0 | 2.9 | 78.85 | 5 | 11.50 | 23.71 | 356.2 | 78.14 | |
| 石川 | 66 | 7 | 12 | 16 | 10.6 | 28.8 | 24.2 | 75.36 | 21 | 11.28 | 23.17 | 404.8 | 77.10 | |
| 愛媛 | 59 | 11 | 17 | 17 | 18.6 | 47.5 | 28.8 | 78.13 | 8 | 11.24 | 23.35 | 440.1 | 86.80 | A2 |
| 埼玉 | 70 | 1 | 7 | 2 | 1.4 | 11.4 | 2.9 | 73.34 | 47 | 11.70 | 23.62 | 296.5 | 73.17 | |
| 広島 | 71 | 14 | 8 | 17 | 19.7 | 31.0 | 23.9 | 77.22 | 11 | 11.71 | 23.78 | 369.9 | 72.00 | |
| 神奈川 | 67 | 6 | 9 | 8 | 9.0 | 22.4 | 11.9 | 74.38 | 33 | 11.62 | 23.94 | 338.1 | 78.14 | |
| 静岡 | 47 | 5 | 5 | 7 | 10.6 | 21.3 | 14.9 | 74.95 | 26 | 11.29 | 23.32 | 372.3 | 78.62 | |
| 福岡 | 67 | 2 | 1 | 9 | 3.0 | 4.5 | 13.4 | 71.25 | 57 | 11.35 | 23.49 | 345.1 | 76.52 | |
| 福島 | 66 | 2 | 6 | 2 | 3.0 | 12.1 | 3.0 | 73.46 | 46 | 11.63 | 23.55 | 303.7 | 76.38 | |
| 神奈川 | 64 | 21 | 13 | 2 | 32.8 | 53.1 | 3.1 | 78.59 | 7 | 11.62 | 23.96 | 349.9 | 73.00 | |
| 熊本 | 52 | 3 | 5 | 2 | 5.8 | 15.4 | 3.9 | 75.17 | 24 | 11.64 | 23.93 | 308.5 | 74.52 | |
| 千葉 | 61 | 2 | 7 | 0 | 3.3 | 14.8 | 0.0 | 73.03 | 49 | 11.66 | 23.69 | 296.4 | 74.11 | |
| 三重 | 71 | 6 | 8 | 1 | 8.4 | 19.7 | 1.4 | 74.21 | 35 | 11.29 | 23.21 | 336.9 | 66.40 | |
| 愛媛 | 59 | 4 | 7 | 4 | 6.8 | 18.6 | 6.8 | 74.11 | 37 | 11.44 | 23.30 | 336.4 | 77.10 | |
| 千葉 | 67 | 14 | 6 | 12 | 20.9 | 29.9 | 17.9 | 74.91 | 27 | 11.36 | 23.28 | 383.3 | 83.61 | A2 |
| 山形 | 53 | 2 | 2 | 2 | 3.8 | 7.5 | 3.8 | 72.79 | 52 | 11.50 | 23.88 | 311.5 | 73.48 | |
| 長崎 | 45 | 19 | 10 | 29 | 42.2 | 64.4 | 64.4 | 80.08 | 2 | 10.94 | 22.49 | 573.4 | 89.48 | A2 |
| 埼玉 | 67 | 1 | 1 | 0 | 1.5 | 3.0 | 0.0 | 70.50 | 60 | 11.99 | 24.95 | 255.5 | 67.86 | |
| 山口 | 62 | 7 | 5 | 3 | 11.3 | 19.4 | 4.8 | 74.61 | 29 | 11.66 | 24.28 | 313.6 | 77.71 | |
| 高知 | 63 | 6 | 4 | 2 | 9.5 | 15.9 | 3.2 | 74.39 | 32 | 11.72 | 23.82 | 300.5 | 73.91 | |
| 静岡 | 68 | 3 | 6 | 6 | 4.4 | 13.2 | 8.8 | 73.55 | 44 | 11.19 | 23.41 | 356.8 | 77.48 | |
| 和歌山 | 67 | 11 | 10 | 2 | 16.4 | 31.3 | 3.0 | 75.61 | 19 | 11.65 | 24.08 | 323.0 | 74.52 | |
| 千葉 | 71 | 3 | 9 | 1 | 4.2 | 16.9 | 1.4 | 75.21 | 23 | 11.77 | 24.19 | 293.0 | 77.48 | |
| 高知 | 66 | 11 | 9 | 13 | 16.7 | 30.3 | 19.7 | 75.87 | 16 | 11.61 | 23.76 | 367.0 | 73.43 | |
| 石川 | 67 | 15 | 15 | 11 | 22.4 | 44.8 | 16.4 | 77.91 | 10 | 11.53 | 23.82 | 381.6 | 75.95 | |
| 広島 | 68 | 5 | 4 | 19 | 7.3 | 13.2 | 27.9 | 73.80 | 40 | 11.51 | 23.77 | 377.4 | 74.62 | |
| 愛媛 | 69 | 30 | 13 | 11 | 43.5 | 62.3 | 15.9 | 78.65 | 6 | 11.28 | 23.29 | 420.9 | 86.81 | A2 |
| 福島 | 64 | 3 | 7 | 2 | 4.7 | 15.6 | 3.1 | 74.51 | 30 | 11.45 | 23.88 | 323.1 | 78.14 | |
| 長崎 | 72 | 8 | 11 | 0 | 11.1 | 26.4 | 0.0 | 75.06 | 25 | 11.59 | 23.94 | 315.2 | 75.43 | |
| 岐阜 | 46 | 6 | 5 | 6 | 13.0 | 23.9 | 13.0 | 74.80 | 28 | 11.34 | 23.49 | 366.3 | 78.24 | |
| 神奈川 | 72 | 31 | 13 | 13 | 43.1 | 61.1 | 18.1 | 78.94 | 4 | 11.53 | 24.37 | 403.6 | 75.95 | |
| 兵庫 | 68 | 3 | 8 | 5 | 4.4 | 16.2 | 7.3 | 75.39 | 20 | 11.76 | 24.50 | 307.9 | 67.10 | |
| 秋田 | 70 | 13 | 13 | 11 | 18.6 | 37.1 | 15.7 | 77.14 | 12 | 11.54 | 23.80 | 370.5 | 77.00 | |
| 京都 | 70 | 13 | 11 | 12 | 18.6 | 34.3 | 17.1 | 76.74 | 14 | 11.40 | 23.68 | 382.9 | 76.57 | |
| 高知 | 64 | 0 | 3 | 0 | 0.0 | 4.7 | 0.0 | 73.79 | 41 | 11.70 | 24.32 | 282.0 | 64.81 | |
| 長崎 | 72 | 4 | 7 | 0 | 5.6 | 15.3 | 0.0 | 73.63 | 42 | 11.75 | 23.77 | 289.4 | 70.33 | |
| 静岡 | 63 | 2 | 1 | 5 | 3.2 | 4.8 | 7.9 | 71.17 | 58 | 11.31 | 24.08 | 335.0 | 74.67 | |
| 群馬 | 62 | 0 | 2 | 11 | 0.0 | 3.2 | 17.7 | 70.00 | 61 | 11.51 | 23.57 | 340.9 | 74.30 | |
| 福岡 | 60 | 8 | 9 | 3 | 13.3 | 28.3 | 5.0 | 75.93 | 15 | 11.62 | 23.64 | 327.3 | 68.19 | |
| 和歌山 | 46 | 23 | 11 | 22 | 50.0 | 73.9 | 47.8 | 79.17 | 3 | 11.10 | 22.75 | 528.7 | 79.00 | |
| 大阪 | 61 | 0 | 19 | 3 | 0.0 | 31.1 | 4.9 | 76.90 | 13 | 11.60 | 23.91 | 331.9 | 72.70 | |
| 千葉 | 62 | 2 | 7 | 2 | 3.2 | 14.5 | 3.2 | 73.61 | 43 | 11.64 | 24.52 | 306.0 | 71.48 | |
| 静岡 | 72 | 0 | 1 | 2 | 0.0 | 1.4 | 2.8 | 71.29 | 56 | 11.59 | 24.14 | 294.6 | 65.16 | |
| 愛媛 | 62 | 19 | 16 | 24 | 30.6 | 56.5 | 38.7 | 78.06 | 9 | 11.03 | 22.66 | 492.6 | 78.81 | |
| 岡山 | 44 | 35 | 7 | 1 | 79.5 | 95.5 | 2.3 | 81.59 | 1 | 11.48 | 24.06 | 406.2 | 77.00 | |
| 福岡 | 63 | 12 | 9 | 20 | 19.1 | 33.3 | 31.8 | 75.23 | 22 | 11.20 | 23.64 | 435.3 | 77.95 | |
| 徳島 | 65 | 3 | 6 | 14 | 4.6 | 13.9 | 21.5 | 72.86 | 51 | 11.76 | 24.33 | 340.8 | 77.86 | |
| 三重 | 64 | 5 | 9 | 13 | 7.8 | 21.9 | 20.3 | 74.06 | 39 | 11.56 | 24.00 | 363.6 | 77.67 | |
| 佐賀 | 70 | 2 | 5 | 7 | 2.9 | 10.0 | 10.0 | 72.74 | 53 | 11.39 | 23.55 | 339.2 | 78.24 | |
| 茨城 | 68 | 9 | 4 | 9 | 13.2 | 19.1 | 13.2 | 72.97 | 50 | 11.59 | 23.66 | 340.3 | 79.10 | |
在校成績の項目とデビュー後7場所の競走得点との相関係数を計算すると、次のとおりとなります。
| 勝率 | vs | デビュー後 7場所の競走得点 |
0.471 |
| 連対率 | vs | 〃 | 0.522 |
| バック取得率 | vs | 〃 | 0.603 |
| 200m独走タイム | vs | 〃 | -0.633 |
| 400m独走タイム | vs | 〃 | -0.605 |
| 訓練競走得点 | vs | 〃 | 0.470 |
相関係数は2つの変数の因果関係の程度を示す数値で、-1~+1の値を取ります。0に近い時には 因果関係がなく、±1に近づくにつれて因果関係 が大きいことを示します。
どうでしょう、勝率・連対率や訓練競走の競走得点より、バック取得率や200m・400mのタイムのほうがデビュー後実績との相関係数が高くなっています。
つまり、在校時に追い込み戦法で在校時の勝率・連対率および訓練得点を上げるより、できるだけ逃げる競走に徹し、脚力をつけることに務めた選手のほうがデビュー後の成績が良いようです。
さらに、統計的手法を用いて在校成績の項目を組み合わせると、デビュー後実績との相関をもっと高める式を得ることができます。
結果だけを示すと、
在校時の総合点(\(Zscore\)) を
- \(ZrtP\)
- 競走訓練における連対率
- \(ZrtB\)
- 競走訓練におけるバック取得率
- \(Z2tm\)
- 在校時の 200m独走最高タイム
- \(Av2T\)
- 同期生全体の 200m独走最高タイム平均値
とすると、総合点(\(Zscore\)) vs デビュー後7場所競走得点 の相関係数は 0.701となり、一般的に言われている「強い相関を示す(相関係数>7.0)」レベルまで達します。
(表1-1. の在校成績・総合点の項目に各選手の総合点計算値を記載しています。)
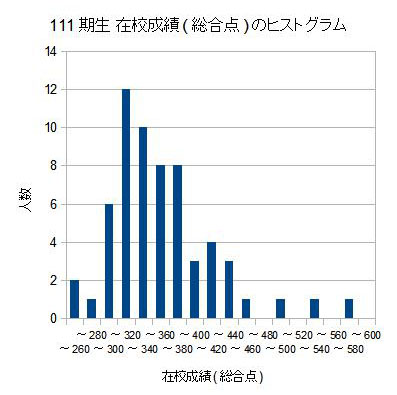
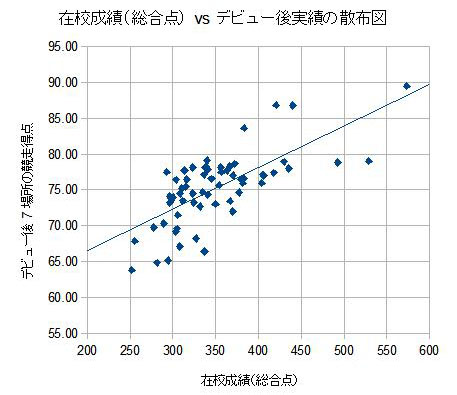
「在校成績総合点(\(Zscore\))のヒストグラム」と、「在校成績総合点(\(Zscore\)) vs デビュー後7場所の競走得点の散布図」を下に示します。
ちなみに、上のヒストグラムで三人の選手が抜けているのが分かると思います。
在校成績総合点の上位から順に、山崎賢人 選手(長崎)、南 潤 選手(和歌山)、松本貴治 選手(愛媛)です。
分析記事作成時の2018年6月現在 デビューからまだ1年経っていませんが、三人とも既にS級に上がり大活躍しています。
さて、上の(1-1)式の説明に、総合点(ZScore) と デビュー後7場所競走得点 の相関係数は 0.701と書きましたが、これは直線の式で相関関係を求めた場合の値です。
右上図の散布状態をみると、自然対数の曲線をあてはめるとさらに相関関係を高めることができそうです。
回帰分析で自然対数の関係式を求めると、
- \(Riscore\)
- デビュー後の初期競走得点
- \(ZScore\)
- 在校時総合点
となります。 この場合、決定係数(R2) = 0.534 で、 相関係数に換算すると 0.730 です。
同様な方法で、デビュー後のT指数見積もり式を求めると、
- \(Tiscore\)
- デビュー後の初期T指数
- \(ZScore\)
- 在校時総合点
となります。この場合、決定係数(R2) = 0.526 で、 相関係数に換算すると 0.725 です。
(T指数はGambooで今後公開される予想情報で、選手の能力を表す指数です。)
今回はここまでです。
次回は上の 総合点(\(Zscore\)) と (1-2),(1-3)式を今年デビューする 113期生の在校成績に適用して、デビュー後の成績を予測します。